Understanding Model Selection with Cross Validation
Introduction:
In machine learning, model selection plays a crucial role in creating models that generalize well to new, unseen data. One common approach to model selection is through cross-validation, a resampling method that helps estimate the performance of a model on different subsets of the dataset. This blog post will explore the concepts of cross-validation and nested cross-validation, providing insights into their significance in the model selection process.
Model Selection:
Model selection involves finding the best-performing model for a given problem. It encompasses choosing optimal hyperparameters, selecting relevant features, and comparing different types of models. A crucial aspect of model selection is avoiding overfitting, where a model performs well on training data but fails to generalize to new data.
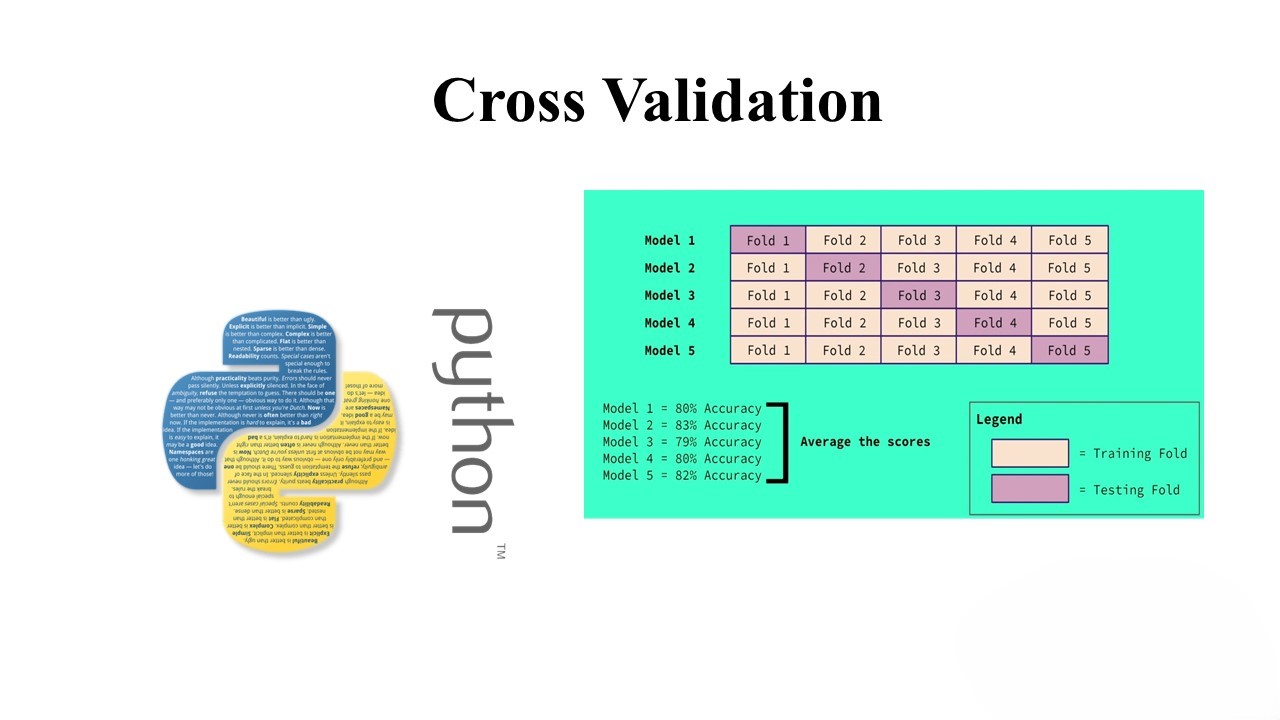
Overview of k-fold Cross Validation:
K-fold cross-validation is a widely used resampling method. In this technique, the dataset is divided into k folds, and the model is trained and tested k times. Each time, one fold is used for testing, and the remaining k-1 folds are used for training. This process helps provide a more robust estimate of the model’s performance. The mean performance over the k folds is often used as the final performance metric.
Introduction to Nested Cross Validation:
Simple cross-validation alone may lead to biased model selection. Nested cross-validation addresses this issue by incorporating two sets of folds: an outer loop for model evaluation and an inner loop for model selection. The outer loop evaluates the model on one set of folds, while the inner loop performs model selection on another set, preventing biased estimates of model performance.
Cross Validation and Computational Efficiency:
While cross-validation is a powerful tool, it can be computationally intensive. The number of folds impacts computational resources, and a balance must be struck between accuracy and efficiency. K-fold cross-validation is a practical compromise, providing a reasonable bias-variance trade-off for most scenarios.
Example: Logistic Regression Model:
Let’s walk through an example using logistic regression for binary classification. We’ll explore how to implement k-fold cross-validation, optimize hyperparameters with nested cross-validation, and evaluate the final model.
#(Code snippets from the provided content)
# Load necessary packages and preprocessed data
import pandas as pd
import sklearn.model_selection as ms
from sklearn import linear_model
import sklearn.metrics as sklm
from sklearn import cross_validation
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
import math
# Load Features and Labels
Features = np.array(pd.read_csv('Credit_Features.csv'))
Labels = np.array(pd.read_csv('Credit_Labels.csv'))
# Create a logistic regression model without cross-validation
X_train, X_test, y_train, y_test = ms.train_test_split(Features, Labels, test_size=300, random_state=1115)
logistic_mod = linear_model.LogisticRegression(C=1.0, class_weight={0: 0.45, 1: 0.55})
logistic_mod.fit(X_train, y_train)
probabilities = logistic_mod.predict_proba(X_test)
# Evaluate the model
print_metrics(y_test, probabilities, 0.3)
plot_auc(y_test, probabilities)
# Perform k-fold cross-validation
scoring = ['precision_macro', 'recall_macro', 'roc_auc']
logistic_mod = linear_model.LogisticRegression(C=1.0, class_weight={0: 0.45, 1: 0.55})
scores = ms.cross_validate(logistic_mod, Features, Labels, scoring=scoring, cv=10, return_train_score=False)
# Display cross-validation results
print_cv(scores)
# Optimize hyperparameters with nested cross-validation
inside = ms.KFold(n_splits=10, shuffle=True)
outside = ms.KFold(n_splits=10, shuffle=True)
param_grid = {"C": [0.1, 1, 10, 100, 1000]}
logistic_mod = linear_model.LogisticRegression(class_weight={0: 0.45, 0: 0.55})
clf = ms.GridSearchCV(estimator=logistic_mod, param_grid=param_grid,
cv=inside, scoring='roc_auc', return_train_score=True)
# Fit the cross-validated grid search
clf.fit(Features, Labels)
# Display results of hyperparameter optimization
plot_cv(clf, param_grid)
# Evaluate the 'best' model with outer loop of nested cross-validation
nr.seed(498)
cv_estimate = ms.cross_val_score(clf, Features, Labels, cv=outside)
print('Mean performance metric = %4.3f' % np.mean(cv_estimate))
print('SDT of the metric = %4.3f' % np.std(cv_estimate))
print('Outcomes by cv fold')
for i, x in enumerate(cv_estimate):
print('Fold %2d %4.3f' % (i + 1, x))
# Build and test the final model with optimal hyperparameters
logistic_mod = linear_model.LogisticRegression(C=0.1, class_weight={0: 0.45, 1: 0.55})
logistic_mod.fit(X_train, y_train)
probabilities = logistic_mod.predict_proba(X_test)
print_metrics(y_test, probabilities, 0.3)
plot_auc(y_test, probabilities)
Summary:
This blog post provided an in-depth understanding of model selection using cross-validation and nested cross-validation. Key takeaways include the importance of resampling methods, the impact of computational efficiency, and the significance of unbiased model evaluation. The logistic regression example demonstrated practical implementation steps, highlighting the variability in model performance and the necessity of nested cross-validation for optimal hyperparameter selection.
In conclusion, model selection is a critical step in building robust machine learning models, and leveraging cross-validation techniques ensures reliable performance estimation.